
(6) Realiza las siguientes operaciones mediante la carndinalidad de los siguienes conjuntos:
Siendo #(A)=2, #(B)=5, #(C)=20 realiza la siguientes operaciones.
1. [Ejercicio 41]
Si (A ∩ B) son disjuntos, #(A ∩ B)
#(A ∩ B)= #(A) + #(B) - #(A ∩ B)
#(A ∩ B)= 2 + 5- 0
#(A ∩ B)= 7
2. [Ejercicio 42]
Si C es disjunto a (A ∩ B) y A={a,b} y B={b, c, d, f, g}, ¿Cual es la cardinalidad de # ((A ∩ B) ∪ C)?
3. [Ejercicio 43]
Si A={a,b}, B={b, c, d, f, g} y C={a, b, c, d, e, f, g, h, i, j, k, l, m, ñ, o, p, r, s , t, v} ¿Cúal es la cardinalidad de
# ((B ∩ C) ∪ A) ?
B ⊂ C, por tanto, la cardinalidad de #(B ∩ C) será la cardinalidad de #(C)
#(B ∩ C) = 20
A ⊂ C, por tanto, #(B ∩ C) = #((B ∩ C) ∪ #(A))
#((B ∩ C) ∪ #(A))=20
4. [Ejercicio 44] Siendo todos los conjuntos disjuntos calcula
#((A∪ B) - (A ∩ B))
5. [Ejercicio 45]
Si C es disjunto y A y B tienen dos elementos en común, calcula
#([(A ∩ B) ∪ C)] - [(B ∩ C) ∪ A])?
| (A ∩ B) ∪ C) | (B ∩ C) ∪ A |
|---|---|
#(A)=2, #(B)=5, #(C)=20 A ⊂ B #(A ∩ B)= 5 #(A ∩ B) = 5 #((A ∩ B) ∪ C)= 25 |
#(A)=2, #(B)=5, #(C)=20 #((B ∩ C))= 25 #(A)=2 A ⊂ B #((B ∩ C) ∪ A)= 25 |
#([(A ∩ B) ∪ C] - [(B ∩ C) ∪ A)])= 25 - 25= 0 |
|
#([(A ∩ B) ∪ C)] - [(B ∩ C) ∪ A])= 0
Problemas de cardinalidad de conjuntos:
6. [Ejercicio 46] Supongamos que una entidad bancaria ha realizado una encuesta acerca de la situación económica de las familias españolas. Según los resultados de la encuesta, el 30% de las familias pagaban un crédito hipotecario, el 40% pagaban un crédito para comprar un coche y el 10% pagaban créditos de ambos. La entidad desea saber qué porcentaje de familias no pagan ni créditos hipotecarios ni créditos para la compra de un coche.
Solución:
Por proporcionalidad, basta razonar sobre un universo de 100 familias. Llamemos a A al conjunto de familias, entre las 100, que están pagando un crédito hipotecario y B al conjunto de familias que pagan un crédito para la compra de un coche. Según los datos, de cada 100 familias 30 pertenecen a A y 40 pertenecen a B, por tanto, #(A)=40 y #(B)=30 luego #(A ∩ B)= 10. Entonces, las que pagan alguno de los créditos serán:
#(A ∪ B) = #(A) + #(B) - #(A ∩ B)
= 30 + 40 - 10
=60
y las que no pagan ninguno de los dos créditos serán
#((A ∪ B)c) = #(U) - #((A ∪ B))= 100 - 60= 40
7. [Ejercicio 47]
8. [Ejercicio 48] Supongamos que en una reunión hay 40 personas que hablan alguno de los idiomas alemán, español o inglés. Se sabe que 22 hablan alemán, 26 no hablan ingles 30 hablan sólo un idioma, 30 hablan ingles o alemán, 7 hablan inglés pero no hablan español y 17 hablan alemán pero no hablan español. Se desea responde a preguntas como ¿Cuantás personas hablan los tres idiomas?¿Cuántas personas hablan sólo español?¿Cuántas hablan español pero no hablan ingles?
Solución:
Llamemos A, B y C, respectivamente, a los conjuntos d personas que hablan alemán, español e ingles. A todas las relaciones entre estos conjuntos podemos representarlas en un diagrama de Venn:
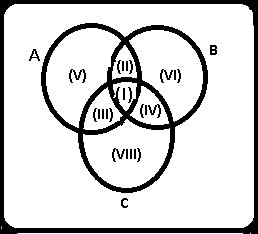
Si formalizamos los datos que aparecen en el ununciado nos quedarán los siguientes datos:
| Número | Enunciado | Formalización | Cardinalidad | Cantidad |
|---|---|---|---|---|
| 1 | Personas en Total | A ∩ B ∩ Cc | #(I) +#(II) +#(III) +#(IV) +#(V) +#(VI) +#(VII) = | 40 |
| 2 | Hablan alemán | A ∩ B ∩ Cc | #(I) +#(II) +#(III) +#(V)= | 22 |
| 3 | No hablán ingles | A ∩ Bc ∩ C | #(II) +#(V) +#(VI)= | 26 |
| 4 | Hablan sólo un idioma | Ac ∩ B ∩ C | #(V) +#(VI)+#(VII)= | 30 |
| 5 | Hablan inglés o alemán | A ∩ Bc ∩ Cc | #(I) +#(II) +#(III) +#(IV) +#(V) +#(VII) = | 30 |
| 6 | Hablan ingles pero no español | Ac ∩ B ∩ Cc | #(III) + #(VII) = | 7 |
| 7 | Hablan alemán pero no español | Ac∩ Bc ∩ Cc | #(III) + #(V) = | 17 |
¿Cuántas personas hablan sólo español?
Responder esto es sencillo. (2) son los que hablan Ingles o Alemán. Si restamos (2) al número total de personas (1) nos queda el número de personas que sólo hablan español.
(1)= #(I) +#(II) +#(III) +#(IV) +#(V) + #(VI) #(VII) =40
(2)= #(I) +#(II) +#(III) +#(IV) +#(V) +#(VII) = 30
#(VI)=#(1)-#(2)
#(VI)=10
Las personas que sólo hablan en español son 10.
¿Cuántas personas hablan los tres idiomas?
Para descubrir esta cifra es necesario realizar más operaciones... Observemos el número de personas que hablan sólo un idioma (4)
#(4)= #(V) + #(VI) +#(VII) = 30
#(VI)= 10
#(V) + #(VII) = 20
Sabemos que 10 personas sólo hablan español. Por tanto, podemos deducir que 20 personas o bien, hablan ingles o bien, hablan alemán.
Ahora vamos a descubrir el número de personas que hablan ingles pero no español y el número de personas que hablan alemán pero no español. Y con este dato, junto a nuestro conocimiento del número de hablantes que sólo hablan ingles o sólo hablan alemán deduciremos los que hablan español y ingles:
#(6) +#(7)= 2x#(III) +#(V) + #(VII)=24
#(V)+#(VII)=20
2x#(III)=4
#(III)=2
Ya sabemos que el número de personas que hablan español y alemán son 4 (#III). Ahora es fácil deducir los que hablan sólo ingles y los que hablan sólo alemán.
#(6)= #(III) +#(VII)=7
#(III)=2
#(VII)=5
3 personas sólo hablan ingles (#VII).
#(7)= #(III) + #(V)=17
#(III)=2
#(V)=15
15 son los que hablan alemán.
Sabiendo los que no hablan ingles #(2) y los que hablan alemán #(V) y los que hablan sólo español #(VI), podemos deducir aquellos que hablan alemán y español #(II).
#(3)=#(II) + #(V) +#(VI)=26
#(V)= 15
#(VI)= 10
Por tanto, #(II)=1
Como sabemos los que hablan alemán #(2), los que hablan alemán y español #(II), los que hablan ingles y alemán #(III) y, por último, los que hablan sólo alemán #(V), podemos deducir definitivamente el número de personas que hablan los tres idiomas.
#(2)=#(I)+#(II)+#(III)+#(V)=22
#(II)=1
#(III)=2
#(V)=15
Por tanto, #(I)= 4
¿Cuantas personas hablan español pero no ingles?
Primero deduciremos el valor de #(IV) mediante los datos disponibles y mediante #(5):
#(5)= #(I) +#(II) +#(III) +#(IV) +#(V) +#(VII) = 30
#(I)= 4
#(II)= 1
#(III)= 2
#(V) = 15
#(VII)= 5
Por tanto, #(IV)= 3
y con este dato deducimos mediante esta operación el número de españoles que no saben ingles:
#(IV) + #(VI)=
#(IV)=3
#(VI)=10
15
El número de Españoles que no saben ingles es de 15.
¡Ejercicio resuelto!
9. [Ejercicio 49] De una encuesta se desprende que uno de cada cuatro españoles es aficionado al fútbol y que uno de cada diez es aficionado al baloncesto. No se dispone de datos acerca de cuántos españoles de datos acerca de cuántos españoles comparten ambas aficiones. En estas circunstancias no se puede averiguar con exactitud cuántos españoles tiene algunas de las dos aficiones no será superior a la suma de las aficiones al fútbol y los aficionados al baloncesto. Como, de cada 100 españoles, hay 25 aficionados al fútbol y 10 aficionados al baloncesto, puede asegurarse que el porcentaje de españoles que tienen alguna de esas aficiones no supera el 35%.
10. [Ejercicio 50] Si el 80% de los alumnos de un curso aprueban la asignatura X y el 70% aprueba la asignatura Y, de cada 100 alumnos, el conjunto A de aprobados en X tiene cardinalidad 80 y el conjunto B de aprobados en Y tiene cardinalidad 70, ¿Cuántos han aprobado dos las dos asignaturas?
Solución:
#(A ∩ B) ≥ #(A) +#(B) -#(U)= 80 + 70 -100=50
Por tanto, al menos el 50% de los alumnos habrán aprobado las dos asignaturas.
¿Quieres conocer al profesor de lógica formal de la Academia LAP?
Regresar
Por favor, dejad vuestra opinión sobre los ejercicios de la página web para que pueda mejorarlos o ampliarlos. ¡Muchísimas gracias a todos! < <
Comentarios, sugerencias y críticas




